CARDANO

 Gerolamo Cardano, o Girolamo Cardano (24 de septiembre de 1501 - 21 de septiembre de 1576) fue un médico notable, además de un célebre matemático italiano del Renacimiento, un astrólogo de valía, y un estudioso del azar. Este filósofo y destacado enciclopedista, fue autor de una de las primeras autobiografías modernas.Nacido en Pavía, Italia, Gerolamo Cardano era hijo ilegítimo de Fazio Cardano, un abogado con talento para las matemáticas que fue amigo de Leonardo Da Vinci. En 1520, entró en la Universidad de Pavía y estudió medicina en Padua consiguiendo excelentes calificaciones. Finalmente, obtuvo una considerable reputación como médico en Saccolongo (cerca de Padua) y sus servicios fueron altamente valorados en las cortes (atendió al Papa y al arzobispo escocés de St. Andrews). No obstante los obstáculos, fue aceptado en 1539 en el Colegio Médico de Milán, llegando a la cúspide de su profesión.Como médico en la medicina renacentista ha sido estudiado agudamente por N. Siraisi, en The Clock and the Mirror. Fue Cardano el primero en describir la fiebre tifoidea y sobre otros temas médicos, como comentarios a Galeno e Hipócrates. Su Contradicentium medicorum, de 1536, aborda temas de discusión en la medicina del siglo XVI. Su El libro de los sueños es la última onirocrítica de raíces antiguas (que culminó con Artemidoro
en el siglo II) y medievales, pasada por el filtro crítico de los
modernos, lo que lo hace un texto valiosísimo; sería citado por Freud en
su Interpretación de los sueños (1900).En primer lugar, destaca por sus trabajos de álgebra. En 1539 publicó su libro de aritmética Practica arithmetica et mensurandi singulares. Publicó las soluciones a las ecuaciones de tercer y cuarto grado en su Ars magna datado en 1545. La solución a un caso particular de ecuación cúbica
Gerolamo Cardano, o Girolamo Cardano (24 de septiembre de 1501 - 21 de septiembre de 1576) fue un médico notable, además de un célebre matemático italiano del Renacimiento, un astrólogo de valía, y un estudioso del azar. Este filósofo y destacado enciclopedista, fue autor de una de las primeras autobiografías modernas.Nacido en Pavía, Italia, Gerolamo Cardano era hijo ilegítimo de Fazio Cardano, un abogado con talento para las matemáticas que fue amigo de Leonardo Da Vinci. En 1520, entró en la Universidad de Pavía y estudió medicina en Padua consiguiendo excelentes calificaciones. Finalmente, obtuvo una considerable reputación como médico en Saccolongo (cerca de Padua) y sus servicios fueron altamente valorados en las cortes (atendió al Papa y al arzobispo escocés de St. Andrews). No obstante los obstáculos, fue aceptado en 1539 en el Colegio Médico de Milán, llegando a la cúspide de su profesión.Como médico en la medicina renacentista ha sido estudiado agudamente por N. Siraisi, en The Clock and the Mirror. Fue Cardano el primero en describir la fiebre tifoidea y sobre otros temas médicos, como comentarios a Galeno e Hipócrates. Su Contradicentium medicorum, de 1536, aborda temas de discusión en la medicina del siglo XVI. Su El libro de los sueños es la última onirocrítica de raíces antiguas (que culminó con Artemidoro
en el siglo II) y medievales, pasada por el filtro crítico de los
modernos, lo que lo hace un texto valiosísimo; sería citado por Freud en
su Interpretación de los sueños (1900).En primer lugar, destaca por sus trabajos de álgebra. En 1539 publicó su libro de aritmética Practica arithmetica et mensurandi singulares. Publicó las soluciones a las ecuaciones de tercer y cuarto grado en su Ars magna datado en 1545. La solución a un caso particular de ecuación cúbica 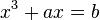 (en notación moderna), le fue comunicada a través de Niccolò Fontana
(más conocido como Tartaglia) a quien Cardano había jurado no desvelar
el secreto de la resolución; no obstante, Cardano consideró que el
juramento había expirado tras obtener información de otras fuentes por
lo que polemizó con Tartaglia, a quien además cita.El método de Cardano es un método para resolver analíticamente cualquier ecuación cúbica y que apareció por primera vez en el libro Ars Magna en 1545 publicado por el matemático italiano Gerolamo Cardano (1501-1576), aunque se dice que fue desarrollado originalmente por los matemáticos italianos Scipione del Ferro (1465-1526) y Niccolò Fontana (1500-1557), éste último apodado Tartaglia (que significa tartamudo). El método es el siguiente.
(en notación moderna), le fue comunicada a través de Niccolò Fontana
(más conocido como Tartaglia) a quien Cardano había jurado no desvelar
el secreto de la resolución; no obstante, Cardano consideró que el
juramento había expirado tras obtener información de otras fuentes por
lo que polemizó con Tartaglia, a quien además cita.El método de Cardano es un método para resolver analíticamente cualquier ecuación cúbica y que apareció por primera vez en el libro Ars Magna en 1545 publicado por el matemático italiano Gerolamo Cardano (1501-1576), aunque se dice que fue desarrollado originalmente por los matemáticos italianos Scipione del Ferro (1465-1526) y Niccolò Fontana (1500-1557), éste último apodado Tartaglia (que significa tartamudo). El método es el siguiente.
La ecuación general de tercer grado
 , y
, y  , se puede convertir en la forma normal dividiendo por
, se puede convertir en la forma normal dividiendo por  y acomodando términos, con lo que queda:
y acomodando términos, con lo que queda:
 se elimina de la forma normal el término cuadrático y se obtiene la forma reducida:
se elimina de la forma normal el término cuadrático y se obtiene la forma reducida:
 , las soluciones de la ecuación original.
, las soluciones de la ecuación original.
 , y
, y  , se puede convertir en la forma normal dividiendo por
, se puede convertir en la forma normal dividiendo por  y acomodando términos, con lo que queda:
y acomodando términos, con lo que queda: se elimina de la forma normal el término cuadrático y se obtiene la forma reducida:
se elimina de la forma normal el término cuadrático y se obtiene la forma reducida: y
y 
 , las soluciones de la ecuación original.
, las soluciones de la ecuación original.Resolución
Partiendo de la ecuación .Entonces
.Entonces y
y  . Llegado a este punto y utilizando las fórmulas de Viète,
. Llegado a este punto y utilizando las fórmulas de Viète, 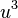 y
y  son las soluciones de la ecuación de segundo grado
son las soluciones de la ecuación de segundo grado y se estudia su signo. Dependiendo de si es positivo, negativo o cero se obtendrán unas soluciones u otras.
y se estudia su signo. Dependiendo de si es positivo, negativo o cero se obtendrán unas soluciones u otras.Si Δ es positivo
La ecuación posee entonces una solución real y dos complejas. Si se establece que . Además, existen dos soluciones complejas conjugadas :
. Además, existen dos soluciones complejas conjugadas :Si Δ es cero
La ecuación posee entonces dos soluciones reales, una simple y una doble :Si Δ es negativo
La ecuación posee entonces tres soluciones reales. Sin embargo, es necesario hacer una incursión en los números complejos para encontrar todas las soluciones. Las soluciones son la suma de dos complejos conjugados y
y  donde
donde ![u=\sqrt[3]{\frac{-q + i\sqrt{|\Delta|}}{2}}](https://upload.wikimedia.org/math/c/9/d/c9da988c9445d621193a008747685e80.png) y
y  ; es el siguiente conjunto :
; es el siguiente conjunto : en forma trigonométrica, obteniéndose :
en forma trigonométrica, obteniéndose :



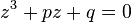



![u = \sqrt[3]{\frac{-q + \sqrt{\Delta}}2}\quad\mbox{y}\quad v = \sqrt[3]{\frac{-q - \sqrt{\Delta}}2}.](https://upload.wikimedia.org/math/3/7/7/3771228383becbe0d75ea757c4fbde59.png)

![\begin{cases}z_0= 2\sqrt[3]{\frac{-q}{2}} = -2\sqrt{\frac{-p}{3}} = \frac{3q}{p} \\ z_1=z_2= -\sqrt[3]{\frac{-q}{2}} = \sqrt{\frac{-p}{3}} = \frac{-3q}{2p} \end{cases}](https://upload.wikimedia.org/math/4/8/4/484e2f397225a3d562e77d359a6b0645.png)


No hay comentarios:
Publicar un comentario