Diofanto de Alejandría

Diofanto de Alejandría, nacido alrededor del 200/214 y fallecido alrededor de 284/298, fue un antiguo matemático griego. Es considerado "el padre del álgebra".

(Siglo III) Matemático griego. Sus escritos contribuyeron de forma notable al perfeccionamiento de la notación algebraica y al desarrollo de los conocimientos del álgebra de su época. Mediante artificios de cálculo supo dar soluciones particulares a numerosos problemas, y estableció las bases para un posterior desarrollo de importantes cuestiones matemáticas. De su obra se conservan varios volúmenes de la Aritmética (libro de inspiración colectiva, pero redactado por un solo autor) y fragmentos de Porismas y Números poligonales.Nacido cerca del 200 d.C. Muere hacia el 284 d.C.)

Hay varias fuentes contradictorias que nos hablan sobre la vida de Diofanto. La fuente que más datos aporta sobre su vida (¡datos que bien pudieran ser ficticios!) es la Antología Griega compilada por Metrodorus hacia el año 500. Esta colección de puzzles histórico-matemáticos incluye uno sobre Diofanto, que dice: "...su infancia duró 1/6 de su vida; se casó después de 1/7 más; su barba creció después de 1/12 más, y su hijo nació 5 años más tarde. El hijo vivió la mitad de años que su padre, y el padre murió 4 años después de la muerte del hijo."
Se llama ecuación diofántica a cualquier ecuación algebraica, de dos o más incógnitas, cuyos coeficientes recorren el conjunto de los números enteros, de las que se buscan soluciones enteras, esto es, que pertenezcan al conjunto de los números enteros.

Un ejemplo de ecuación diofántica es:

x + y = 5 \,

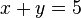
Esta ecuación tiene infinitas soluciones en los números enteros. Como regla general, sin embargo, las ecuaciones que aparecen en los problemas tienen restricciones que nos ayudan a limitarnos a un pequeño número de casos e incluso a una única solución.
Por ejemplo, en nuestra ecuación, si restringimos los posibles valores de