EMMY NOETHER
 Emmy Noether (pronunciado en alemán [ˈnøːtɐ], Erlangen, Baviera, Alemania, 23 de marzo de 1882-Bryn Mawr, Pensilvania, Estados Unidos, 14 de abril de 1935) fue una matemática, judía, alemana de nacimiento, conocida por sus contribuciones de fundamental importancia en los campos de la física teórica y el álgebra abstracta. Considerada por David Hilbert, Albert Einstein y otros personajes como la mujer más importante en la historia de la matemática, revolucionó las teorías de anillos, cuerpos y álgebras. En física, el teorema de Noether explica la conexión fundamental entre la simetría en física y las leyes de conservación.Nació en una familia judía en la ciudad bávara de Erlangen; su padre era el matemático Max Noether. Emmy originalmente pensó en enseñar francés e inglés tras aprobar los exámenes requeridos para ello, pero en su lugar estudió matemáticas en la Universidad de Erlangen-Núremberg, donde su padre impartía clases. Tras defender su tesis bajo la supervisión de Paul Gordan, trabajó en el Instituto Matemático de Erlangen sin percibir retribuciones durante siete años. En 1915 fue invitada por David Hilbert y Felix Klein a entrar en el departamento de matemáticas de la Universidad de Gotinga,
que en ese momento era un centro de investigación matemática de fama
mundial. La facultad de filosofía, sin embargo, puso objeciones a su
puesto y por ello se pasó cuatro años dando clases en nombre de Hilbert.
Su habilitación recibió la aprobación en 1919, permitiéndole obtener el
rango de Privatdozent.La teoría de Galois trata de las transformaciones de cuerpos numéricos que permutan las raíces de una ecuación. Considérese una ecuación polinómica de una variable x de grado n, en el que los coeficientes pertenecen a algún «cuerpo base», que podría ser, por ejemplo, el cuerpo de los números reales, el de los números racionales o el de los enteros módulo 7. Pueden existir o no valores de x que anulen este polinomio. Estos valores, si existen, se llaman raíces. Si el polinomio es x2 + 1 y el cuerpo es el de los números reales, entonces el polinomio no tiene raíces, porque cualquier valor de x hace que el polinomio sea mayor o igual que uno. No obstante, si el cuerpo se extiende,
entonces el polinomio puede tener raíces, y si se le extiende lo
suficiente, tendrá un número de raíces igual a su grado. Continuando con
el ejemplo previo, si el cuerpo se extiende a los números complejos,
entonces el polinomio tiene dos raíces, i y −i, dondei es la unidad imaginaria, esto es, i 2 = −1. De modo más general, la extensión del cuerpo en el que un polinomio puede factorizarse en sus raíces se conoce como cuerpo de descomposición del polinomio
Emmy Noether (pronunciado en alemán [ˈnøːtɐ], Erlangen, Baviera, Alemania, 23 de marzo de 1882-Bryn Mawr, Pensilvania, Estados Unidos, 14 de abril de 1935) fue una matemática, judía, alemana de nacimiento, conocida por sus contribuciones de fundamental importancia en los campos de la física teórica y el álgebra abstracta. Considerada por David Hilbert, Albert Einstein y otros personajes como la mujer más importante en la historia de la matemática, revolucionó las teorías de anillos, cuerpos y álgebras. En física, el teorema de Noether explica la conexión fundamental entre la simetría en física y las leyes de conservación.Nació en una familia judía en la ciudad bávara de Erlangen; su padre era el matemático Max Noether. Emmy originalmente pensó en enseñar francés e inglés tras aprobar los exámenes requeridos para ello, pero en su lugar estudió matemáticas en la Universidad de Erlangen-Núremberg, donde su padre impartía clases. Tras defender su tesis bajo la supervisión de Paul Gordan, trabajó en el Instituto Matemático de Erlangen sin percibir retribuciones durante siete años. En 1915 fue invitada por David Hilbert y Felix Klein a entrar en el departamento de matemáticas de la Universidad de Gotinga,
que en ese momento era un centro de investigación matemática de fama
mundial. La facultad de filosofía, sin embargo, puso objeciones a su
puesto y por ello se pasó cuatro años dando clases en nombre de Hilbert.
Su habilitación recibió la aprobación en 1919, permitiéndole obtener el
rango de Privatdozent.La teoría de Galois trata de las transformaciones de cuerpos numéricos que permutan las raíces de una ecuación. Considérese una ecuación polinómica de una variable x de grado n, en el que los coeficientes pertenecen a algún «cuerpo base», que podría ser, por ejemplo, el cuerpo de los números reales, el de los números racionales o el de los enteros módulo 7. Pueden existir o no valores de x que anulen este polinomio. Estos valores, si existen, se llaman raíces. Si el polinomio es x2 + 1 y el cuerpo es el de los números reales, entonces el polinomio no tiene raíces, porque cualquier valor de x hace que el polinomio sea mayor o igual que uno. No obstante, si el cuerpo se extiende,
entonces el polinomio puede tener raíces, y si se le extiende lo
suficiente, tendrá un número de raíces igual a su grado. Continuando con
el ejemplo previo, si el cuerpo se extiende a los números complejos,
entonces el polinomio tiene dos raíces, i y −i, dondei es la unidad imaginaria, esto es, i 2 = −1. De modo más general, la extensión del cuerpo en el que un polinomio puede factorizarse en sus raíces se conoce como cuerpo de descomposición del polinomio



 ,
,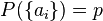 .
.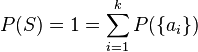 entonces
entonces  .
. entonces
entonces 
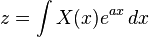
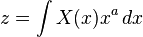





 y
y  son las funciones trigonométricas seno y coseno.
son las funciones trigonométricas seno y coseno.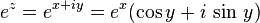
 la variable compleja definida por
la variable compleja definida por